VÍDEO MOTIVADOR

ANGULOS

ÁNGULOS

CONCEPTO

Ángulos adyacentes, los que tienen un vértice y un lado común, y semirrectas opuestas, pero no tienen ningún punto interior común, y suman 180°.Ángulos consecutivos, los que tienen un lado y el vértice común. Ángulos opuestos por el vértice, aquellos cuyos lados son semirrectas opuestas.

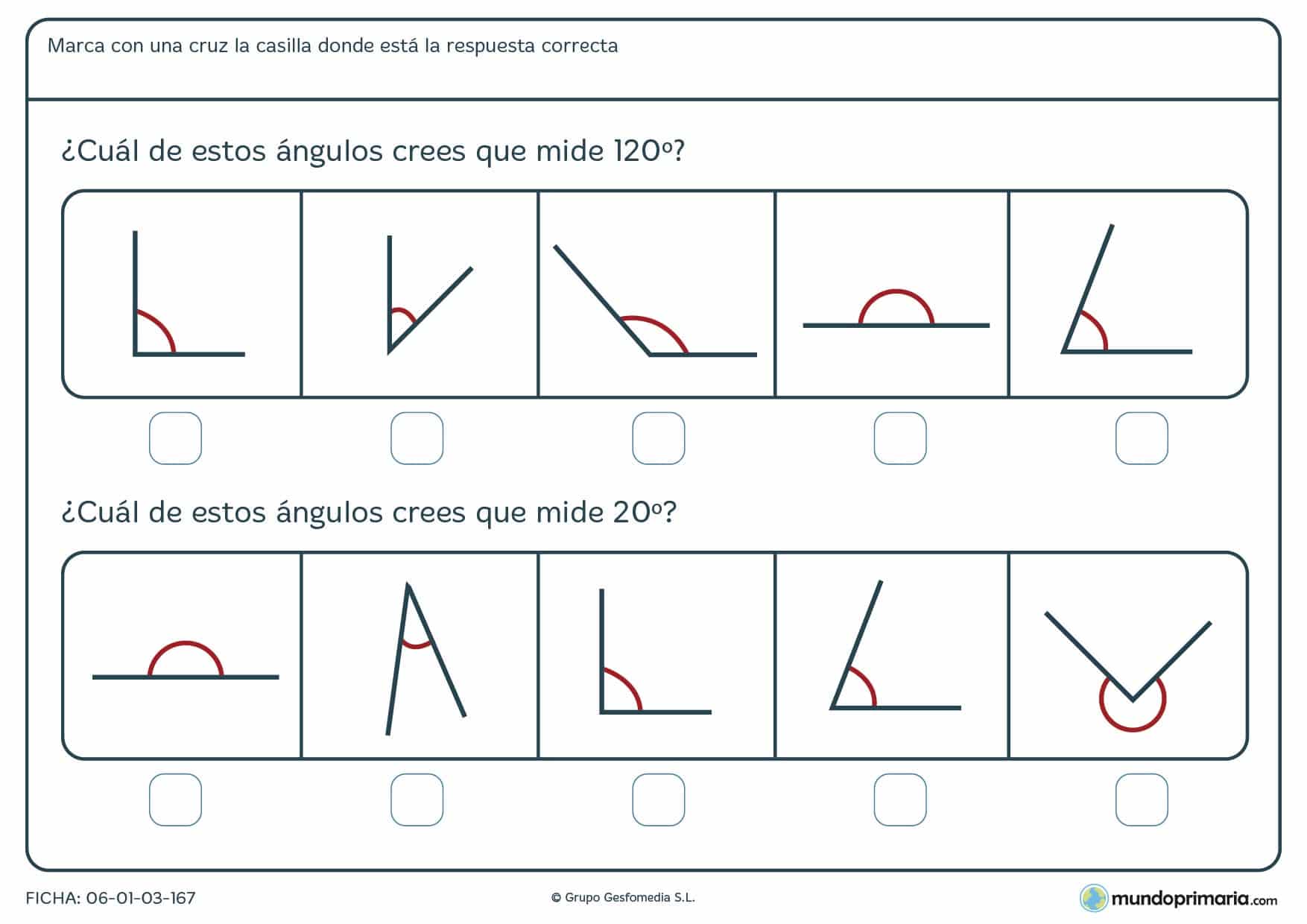
https://es.wikipedia.org/wiki/%C3%81ngulo

RUFFINI

                           MÉTODO DE RUFFINI

CONCEPTO

En matemáticas, la regla de Ruffini facilita el cálculo rápido de la división de cualquier polinomio entre un binomio de la forma {\displaystyle (x-r)\ }. Descrita por Paolo Ruffini en 1809, es un caso especial de división sintética (una división de polinomios en donde el divisor es un «factor lineal»). El Algoritmo de Horner para la división de polinomios utiliza la regla de Ruffini (también se la conoce como Método de Horner o Algoritmo de Ruffini-Horner). La regla de Ruffini permite asimismo localizar las raíces de un polinomio y factorizarlo en binomios de la forma {\displaystyle (x-r)\ } (siendo r un número entero) si es coherente.

EJEMPLOS

1. Se escribe ${\displaystyle Q(x)=x+1=x-(-1)\,\!}$ y el primer coeficiente (2) en el primer renglón:

${\displaystyle {\begin{array}{c|cccc}{}&2&3&0&-4\\-1&{}&{}&{}&{}\\\hline {}&2&{}&{}&{}\\\end{array}}}$

2. Multiplicando por la raíz r=(-1):

${\displaystyle {\begin{array}{c|rrrr}{}&2&3&0&-4\\-1&{}&{-2}&{}&{}\\\hline {}&2&{}&{}&{}\\\end{array}}}$

3. Sumando la columna:

${\displaystyle {\begin{array}{c|rrrr}{}&2&3&0&-4\\-1&{}&{-2}&{}&{}\\\hline {}&2&{1}&{}&{}\\\end{array}}}$

4. El procedimiento se repite hasta obtener el residuo:

${\displaystyle {\begin{array}{c|rrrr}{}&2&3&0&-4\\-1&{}&{-2}&{-1}&{1}\\\hline {}&2&{1}&{-1}&{-3}\\{}&\mathrm {Coef.} &{}&{}&\mathrm {Resto} \end{array}}}$

Si el polinomio original = divisor×cociente+resto, entonces

${\displaystyle P(x)=Q(x)R(x)+s\,\!}$, donde

${\displaystyle R(x)=2x^{2}+x-1\,\!}$ y ${\displaystyle s=-3.\,\!}$

Ejemplo 2

Cuando el resto es igual a 0; permite factorizar, como en el siguiente ejemplo:

${\displaystyle F(x)=x^{3}+x^{2}-x-1}$

Tomamos

${\displaystyle G(x)=x+1}$

Usamos el método, y nos queda así:

${\displaystyle {\begin{array}{c|rrrr}{}&1&1&-1&-1\\-1&{}&{-1}&{0}&{1}\\\hline {}&1&{0}&{-1}&{0}\\{}&\mathrm {Coef.} &{}&{}&\mathrm {Resto} \end{array}}}$

Entonces F(x) se factoriza ${\displaystyle (x^{2}-1)(x+1)}$

Encontrar raíces

Véase también: Teorema de la raíz racional

Si ${\displaystyle P(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+...+a_{1}x+a_{0}}$ es un polinomio con coeficientes enteros y con a₀ y a_n distintos de cero, entonces por el teorema de la raíz racional, todas las raíces racionales reales serán de la forma p/q, donde p es un entero divisor de a₀ y q es un entero divisor de a_n. Así por ejemplo, si el polinomio es

${\displaystyle P(x)=x^{3}+2x^{2}-x-2=0\,\!,}$

entonces las posibles raíces racionales son todos los enteros divisores de a₀ (−2):

${\displaystyle {\text{Posibles raíces:}}\left\{+1,-1,+2,-2\right\}.}$

https://es.wikipedia.org/wiki/Regla_de_Ruffini

FICHA PARA RESOLVER