CONJUNTOS

La teoría de conjuntos es una rama de las matemáticas que estudia las propiedades y relaciones de los conjuntos: colecciones abstractas de objetos, consideradas como objetos en sí mismas. Los conjuntos y sus operaciones más elementales son una herramienta básica en la formulación de cualquier teoría matemática.

Definición
¿Qué es un conjunto? Bueno, por decirlo de una manera simple es una colección. Primero eliges una propiedad común a unas "cosas" (esto lo definiremos luego) y después reúnes las "cosas" que tienen esa propiedad.



Por ejemplo, la ropa que llevas: podrían ser zapatos, calcetines, sombrero, camisa, pantalones y otras cosas.
Esto es un conjunto.
Otro ejemplo sería tipos de dedos.
Este conjunto tendría pulgar, índice, medio, corazón y meñique.



Así que son sólo cosas juntas que tienen una misma propiedad.
Notación
Hay una notación para conjuntos bastante simple. Los dos ejemplos de arriba son:
{calcetines, zapatos, relojes, faldas, ...}
{pulgar, índice, medio, corazón, meñique}
Fíjate que uno tiene "...". Esto sólo quiere decir que el conjunto sigue indefinidamente. A lo mejor no hay infinitas cosas distintas que ponerse, pero no estoy seguro de eso. Después de pensarlo durante una hora, todavía no estoy seguro. El primer conjunto es un conjunto infinito, el segundo es un conjunto finito.
Conjuntos de números
¿Qué tiene esto que ver con matemáticas? Cuando definimos un conjunto, todo lo que hace falta es una propiedad común. ¿Quién dice que no se puede hacer lo mismo con números?

Conjunto de números pares: {..., -4, -2, 0, 2, 4, ...}

Conjunto de números impares: {..., -3, -1, 1, 3, ...}

Conjunto de números primos: {2, 3, 5, 7, 11, 13, 17, ...}

Múltiplos positivos de 3 que son menores que 10: {3, 6, 9}

Y la lista sigue. Podemos inventar muchos conjuntos distintos.
También hay conjuntos de números que no cumplen una propiedad común, simplemente se definen así. Por ejemplo:

{2, 3, 6, 828, 3839, 8827}

{4, 5, 6, 10, 21}

{2, 949, 48282, 42882959, 119484203}

Todos estos conjuntos los he escrito aporreando mi teclado sin mirar.
¿Por qué son importantes los conjuntos?

Los conjuntos son los ladrillos fundamentales de las matemáticas. Es verdad que los conjuntos, por sí solos, no parecen nada del otro mundo. Pero cuando los aplicas en distintas situaciones es cuando se convierten en los bloques con los que las matemáticas se construyen.
De la misma manera que hay conjuntos finitos e infinitos, estos tienen cardinal finito e infinito. Para conjuntos finitos, lo representamos con un número, el número de elementos. Por ejemplo, {1, 2, 3, 4} tiene cardinal 4. Sobre conjuntos infinitos, sólo podemos decir que tienen cardinal infinito. Aunque parezca raro, hay infinitos más grandes que otros, pero este es un tema avanzado en teoría de conjuntos.

http://www.disfrutalasmatematicas.com/conjuntos/conjuntos-introduccion.html

Fracciones

Multiplicación de Fracciones
En la multiplicación de fracciones, las fracciones homogéneas y heterogéneas se multiplican de la misma forma:
   Ejemplo: 2  · 3    =  6  =  2 · 3 _  =   1 
                   3    4       12      3 · 2 ·2      2 
                                             
 
División de Fracciones 
 
En la división de fracciones, siempre se cambia a multiplicación y la segunda fracción cambia a su recíproco. 
 
Ejemplo: 
 
          3  ÷   4   =  3  · 3   =  9 
          5       3        5     4      20 
 
Ejemplo:
    3  ÷  1   =  3 · 2   =  6 
    7      2       7   1        7 

Suma de Fracciones A

Objetivo:

• Suma y resta de fracciones
• Comparación de fracciones utilizando las reglas de proporción

Utilizando un algoritmo sencillo podemos aprender a sumar fracciones mentalmente.

Veamos: Sean a /b   y c/d dos fracciones cualesquiera. Si las deseamos sumar podemos seguir la siguiente regla:

                    

a   +   c   =       ad + bc     (se multiplica cruzado y los productos de suman)       b        d                bd        (se multiplican los denominadores)

Veamos un ejemplo:

             El jefe de Cheo repartió los trabajos de contabilidad de urgencia entre algunos de los contables. A Cheo le tocó una cuarta parte (1/4) de los trabajos de urgencia más la tercera (1/3) parte del trabajo que le iba a tocar al empleado que faltó. En total , ¿qué parte del trabajo tiene que realizar Cheo?

1   +  1    =    1(3) + 4(1)  = 3  + 4   =  7 4        3                (4)(3)           12          12

Paso 1 :   1  + 1    =  ___           = 8> 
                   4     2          8
Paso 2 :  1  + 1   =  (2 ·1) + (4 · 1)   < Se multiplicó cruzado> 
                  4     2                8 
  
 
Paso 3:   2 + 4 =   6      < Se suman los productos para obtener el numerador.> 
                    8          8
Paso 4:  6 ÷  2 =  3     < Se simplifica la fracción si es posible.> 
                 8     2      4 
Resta de Fracciones
    En la resta de fracciones, se utilizan las mismas reglas de la suma de fracciones; pero en este caso hay que restar. 
 
Ejemplo 1: 
 
          5 - 1  = 4         Resta de Fracciones Homogéneas 
          9    9     9
Ejemplo 2:

          2 - 1  =  ( 2 · 2) - (3 · 1)  = 4 - 3   = 1 
           3   2                 6                    6        6 

          

             "PRODUCTOS NOTABLES"

     

Sabemos que se llama producto al resultado de una multiplicación. También sabemos que los valores que se multiplican se llaman factores.

Se llama productos notables a ciertas expresiones algebraicas que se encuentran frecuentemente y que es preciso saber actorizarlas a simple vista; es decir, sin necesidad de hacerlo paso por paso.

Se les llama productos notables (también productos especiales) precisamente porque son muy utilizados en los ejercicios.

 A continuación veremos algunas expresiones algebraicas y del lado derecho de la igualdad se muestra la forma de factorizarlas (mostrada como un producto notable).

Cuadrado de la suma de dos cantidades o binomio cuadrado

a2 + 2ab + b2 = (a + b)2

El cuadrado de la suma de dos cantidades es igual al cuadrado de la primera cantidad, más el doble de la primera cantidad multiplicada por la segunda, más el cuadrado de la segunda cantidad.

Demostración:

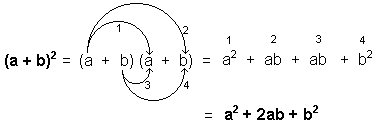
Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma a² + 2ab + b² debemos identificarla de inmediato y saber que podemos factorizarla como (a + b)²

Nota:

Se recomienda volver al tema factorización para reforzar su comprensión.

Ver: PSU; Matemática

Pregunta 12_2005

Cuadrado de la diferencia de dos cantidades

a2 – 2ab + b2 = (a – b)2

El cuadrado de la diferencia de dos cantidades es igual al cuadrado de la primera cantidad, menos el doble de la primera cantidad multiplicada por la segunda, más el cuadrado de la segunda cantidad.

Demostración:

Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma a² – 2ab + b² debemos identificarla de inmediato y saber que podemos factorizarla como (a – b)²

Producto de la suma por la diferencia de dos cantidades (o producto de dos binomios conjugados)

(a + b) (a – b) = a2 – b2

El producto de la suma por la diferencia de dos cantidades es igual al cuadrado de la primera cantidad, menos el cuadrado de la segunda

Demostración:

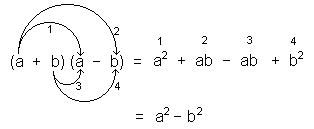
Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma (a + b) (a – b) debemos identificarla de inmediato y saber que podemos factorizarla como a² – b²

Ver: PSU: Matematica,

Pregunta 15_2010

Pregunta 19_2010

Pregunta 09_2006

Otros casos de productos notable (o especiales):

Producto de dos binomios con un término común, de la forma

x2 + (a + b)x + ab = (x + a) (x + b)

Demostración:

Veamos un ejemplo explicativo:

Tenemos la expresión algebraica

x² + 9 x + 14

obtenida del producto entre (x + 2) (x + 7 )

¿Cómo llegamos a la expresión?

a) El cuadrado del término común es (x)(x) = x²

b) La suma de términos no comunes multiplicada por el término común es (2 + 7)x = 9x

c) El producto de los términos no comunes es (2)(7) = 14

Así, tenemos:

x² + 9 x + 14 = (x + 2) (x + 7 )

Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma x² + (a + b)x + ab debemos identificarla de inmediato y saber que podemos factorizarla como (x + a) (x + b)

Producto de dos binomios con un término común, de la forma

x2 + (a – b)x – ab = (x + a) (x – b)

Demostración:

Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma x² + (a – b)x – ab debemos identificarla de inmediato y saber que podemos factorizarla como (x + a) (x – b).

Producto de dos binomios con un término común, de la forma

x2 – (a + b)x + ab = (x – a) (x – b)

Demostración:

Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma x² – (a + b)x + ab debemos identificarla de inmediato y saber que podemos factorizarla como (x – a) (x – b).

Producto de dos binomios con un término común, de la forma

mnx2 + ab + (mb + na)x = (mx + a) (nx + b)

En este caso, vemos que el término común (x) tiene distinto coeficiente en cada binomio (mx y nx).

Demostración:

Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma mnx² + ab + (mb + na)xdebemos identificarla de inmediato y saber que podemos factorizarla como (mx + a) (nx + b).

Cubo de una suma

a3 + 3a2b + 3ab2 + b3 = (a + b)3

Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma a³ + 3a²b + 3ab² + b³debemos identificarla de inmediato y saber que podemos factorizarla como (a + b)³.

Cubo de una diferencia

a3 – 3a2b + 3ab2 – b3 = (a – b)3

Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma a³ – 3a²b + 3ab² – b³debemos identificarla de inmediato y saber que podemos factorizarla como (a – b)³.

A modo de resumen, se entrega el siguiente cuadro con Productos notables y la expresión algebraica que lo representa:

Producto notable		Expresión algebraica	Nombre
(a + b)2	=	a2 + 2ab + b2	Binomio al cuadrado
(a + b)3	=	a3 + 3a2b + 3ab2 + b3	Binomio al cubo
a2 - b2	=	(a + b) (a - b)	Diferencia de cuadrados
a3 - b3	=	(a - b) (a2 + b2 + ab)	Diferencia de cubos
a3 + b3	=	(a + b) (a2 + b2 - ab)	Suma de cubos
a4 - b4	=	(a + b) (a - b) (a2 + b2)	Diferencia cuarta
(a + b + c)2	=	a2 + b2 + c2 + 2ab + 2ac + 2bc	Trinomio al cuadrado

PRODUCTOS NOTABLE :

Algunas formulas: ¬.¬

consiguiendo que te gusten las matematicas

                                   ¿Cómo conseguir que gusten las matemáticas?

Las matemáticas tienen fama de ser densas, difíciles y aburridas. Con las webs y blogs que te presentamos a continuación, podrás despertar la curiosidad y el interés de tus alumnos por esta materia hasta ahora complicada. ¡Toma nota!

1. Sangakoo: Red social en la que puedes interactuar con tus alumnos y facilitarles el aprendizaje de los contenidos matemáticos, al mismo tiempo que ellos generan problemas genuinos.
2. Sector matemática: Web que contiene gran variedad de recursos educativos para el aprendizaje de las matemáticas, clasificados por edades, desde Educación Primaria hasta Educación Secundaria.
3. WIRISmath: Web en la que se pueden crear fórmulas matemáticas en línea y de manera muy sencilla. Ofrece una solución global para el aprendizaje de las matemáticas.
4. Conceptuamath: Web en la que se pueden encontrar numerosos vídeos y aplicaciones que facilitan el aprendizaje y la práctica de conceptos matemáticos.
5. Tocamates: Blog en el que se proponen actividades para practicar las matemáticas a través  de ejercicios en los que es necesaria aplicar la creatividad en la manipulación de objetos.
6. MathTV: Web muy completa para repasar álgebra, cálculo, trigonometría, geometría a través de atractivos vídeos, disponibles la gran mayoría en español.
7. Ematematicas: Web muy extensa en la que puedes darte de alta como docente o como alumno y puedes practicar numerosos ejercicios matemáticos clasificados por temas.
8. Math.cilenia.com: Web destinada a los más pequeños en la que los ejercicios se practican a modo de juego. Están clasificados por niveles de dificultad, de muy fácil a no tan fácil.
9. El abuelo educa: Web en la que el docente podrá encontrar juegos y ejercicios para que sus alumnos aprendan y repasen las materias que más les cuesten.
10. Mathgametime: Web en inglés en la que los ejercicios de matemáticas se plantean a manera de juegos. Una original y divertida manera de hacer atractivas las mates a los más pequeños.
11. Lasmatematicas: Portal dirigido a los alumnos de secundaria que contiene numerosos tutoriales, ejercicios, webs, enlaces interesantes para el aprendizaje de las matemáticas.
12. Retomates: Sitio web dedicado a ultimo ciclo de primaria y la etapa de secundaria. Destinado a alumnos, familias y profesores para aprender de manera divertida.